calculus ref for methods

diff --git a/methods/calculus.md b/methods/calculus.md
index 8cb35215e73c998d11398ef33a8a1502f916203c..8824f9c1d65b04fbf6a12ad8f35f94f053f898fc 100644 (file)
--- a/methods/calculus.md
+++ b/methods/calculus.md
@@ -53,6 +53,8 @@ $$f^\prime(x)=\lim_{h \rightarrow 0}{{f(x+h)-f(x)} \over h}$$
 
 **Tangent line** of function $f$ at point $M(a, f(a))$ is the line through $M$ with gradient $f^\prime(a)$.
 
+For $f(x)=x^n, \hspace{0.5em} f^\prime (x) = nx^{n-1}$
+
 ## Tangents and gradients
 
 
@@ -72,3 +74,23 @@ Normal line for point $P(q,r)$ on function $f$ is $y=mx+c$ where $m={-1 \over m_
 
 **In main**: type function. Interactive -> Calculation -> Line -> (Normal | Tan line)  
 **In graph**: define function. Analysis -> Sketch -> (Normal | Tan line). Type $x$ value to solve for a point. Return to show equation for line.
+
+## Stationary points
+
+Stationary where $m=0$.  
+Find derivative, solve for ${dy \over dx} = 0$
+
+### Type of stationary points
+
+![](https://cdn.edjin.com/upload/RESOURCE/IMAGE/78444.png)
+
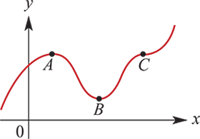
+**Local maximum at point $A$**  
+- $f^\prime (x) > 0$ left of $A$
+- $f^\prime (x) < 0$ right of $A$
+
+**Local minimum at point $B$**  
+- $f^\prime (x) < 0$ left of $B$
+- $f^\prime (x) > 0$ right of $B$
+
+**Stationary** point of inflection at $C$
+