## Average rate of change
+$$m \operatorname{of} x \in [a,b] = {{f(b)-f(a)}\over {b - a}} = {dy \over dx}$$
+
Average rate of change between $x=[a,b]$ given two points $P(a, f(a))$ and $Q(b, f(b))$ is the gradient $m$ of line $\overleftrightarrow{PQ}$
+On CAS: (Action|Interactive) -> Calculation -> Diff -> $f(x)$ or $y=\dots$
+
## Instantaneous rate of change
Tangent to a curve at a point - has same slope as graph at this point.
Values for $\Delta$ are always approximations.
-Secant - line passing through two points on a curve
+Secant - line passing through two points on a curve
Chord - line segment joining two points on a curve
Instantaneous rate of change is estimated by using two given points on each side of the concerned point. Evaluate as in average rate of change.
Each point $Q_n<P$ becomes closer to $Q_P$.
-## Position and velocity
+## Limits and Continuity
-Position - location relative to a reference point
+(see spec notes)
-Average velocity - average rate of change in position over time
+## Position and velocity
+Position - location relative to a reference point
+Average velocity - average rate of change in position over time
Instantaneous velocity - calculated the same way as averge $\Delta$
## Derivatives
$$f^\prime(x)=\lim_{h \rightarrow 0}{{f(x+h)-f(x)} \over h}$$
**Tangent line** of function $f$ at point $M(a, f(a))$ is the line through $M$ with gradient $f^\prime(a)$.
+
+For $f(x)=x^n, \hspace{0.5em} f^\prime (x) = nx^{n-1}$
+
+## Tangents and gradients
+
+
+### Tangent of a point
+
+For a point $P(q,r)$ on function $f$, the gradient of the tangent is the derivative $dy \over dx$ of $f(q)$. Therefore the tangent line is defined by $y=mx+c$ where $m={dy \over dx}$. Substitute $x=q, \hspace{0.5em} y=q$ to solve for $c$.
+
+### Normal
+
+Normal $\perp$ tangent.
+
+$$m_{\operatorname{tan}} \cdot m_{\operatorname{norm}} = -1$$
+
+Normal line for point $P(q,r)$ on function $f$ is $y=mx+c$ where $m={-1 \over m_{\tan}}$. To find $c$, substitute $(x, y)=(q,r)$ and solve.
+
+### Solving on CAS
+
+**In main**: type function. Interactive -> Calculation -> Line -> (Normal | Tan line)
+**In graph**: define function. Analysis -> Sketch -> (Normal | Tan line). Type $x$ value to solve for a point. Return to show equation for line.
+
+## Stationary points
+
+Stationary where $m=0$.
+Find derivative, solve for ${dy \over dx} = 0$
+
+### Type of stationary points
+
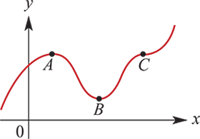
+
+
+**Local maximum at point $A$**
+- $f^\prime (x) > 0$ left of $A$
+- $f^\prime (x) < 0$ right of $A$
+
+**Local minimum at point $B$**
+- $f^\prime (x) < 0$ left of $B$
+- $f^\prime (x) > 0$ right of $B$
+
+**Stationary** point of inflection at $C$
+