## Average rate of change
+$$m \operatorname{of} x \in [a,b] = {{f(b)-f(a)}\over {b - a}} = {dy \over dx}$$
+
Average rate of change between $x=[a,b]$ given two points $P(a, f(a))$ and $Q(b, f(b))$ is the gradient $m$ of line $\overleftrightarrow{PQ}$
+On CAS: (Action|Interactive) -> Calculation -> Diff -> $f(x)$ or $y=\dots$
+
## Instantaneous rate of change
Tangent to a curve at a point - has same slope as graph at this point.
Values for $\Delta$ are always approximations.
**Tangent line** of function $f$ at point $M(a, f(a))$ is the line through $M$ with gradient $f^\prime(a)$.
+For $f(x)=x^n, \hspace{0.5em} f^\prime (x) = nx^{n-1}$
+
## Tangents and gradients
**In main**: type function. Interactive -> Calculation -> Line -> (Normal | Tan line)
**In graph**: define function. Analysis -> Sketch -> (Normal | Tan line). Type $x$ value to solve for a point. Return to show equation for line.
+
+## Stationary points
+
+Stationary where $m=0$.
+Find derivative, solve for ${dy \over dx} = 0$
+
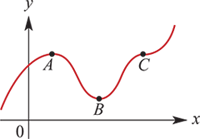
+### Type of stationary points
+
+
+
+**Local maximum at point $A$**
+- $f^\prime (x) > 0$ left of $A$
+- $f^\prime (x) < 0$ right of $A$
+
+**Local minimum at point $B$**
+- $f^\prime (x) < 0$ left of $B$
+- $f^\prime (x) > 0$ right of $B$
+
+**Stationary** point of inflection at $C$
+