calculus (specialist & methods)

diff --git a/methods/calculus.md b/methods/calculus.md
index fb3761fef5a7f5d388d3a3c9322bb385104516c3..c28a4984c384a834a0888aeaa0e38bd366217e9b 100644 (file)
--- a/methods/calculus.md
+++ b/methods/calculus.md
@@ -77,3 +77,18 @@ Normal line for point $P(q,r)$ on function $f$ is $y=mx+c$ where $m={-1 \over m_
 
 Stationary where $m=0$.  
 Find derivative, solve for ${dy \over dx} = 0$
+
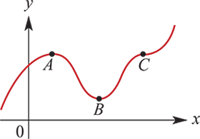
+### Type of stationary points
+
+![](https://cdn.edjin.com/upload/RESOURCE/IMAGE/78444.png)
+
+**Local maximum at point $A$**  
+- $f^\prime (x) > 0$ left of $A$
+- $f^\prime (x) < 0$ right of $A$
+
+**Local minimum at point $B$**  
+- $f^\prime (x) < 0$ left of $B$
+- $f^\prime (x) > 0$ right of $B$
+
+**Stationary** point of inflection at $C$
+

diff --git a/spec/calculus.md b/spec/calculus.md
index 84764124ba5676405e7b4d15738e46af2a6b956a..f98aee74b7997a51b29729e723b9f89cd1f2240a 100644 (file)
--- a/spec/calculus.md
+++ b/spec/calculus.md
@@ -189,8 +189,16 @@ $$\int xn = {x^{n+1} \over n+1} + c$$
 $\int f(x) + g(x) dx = \int f(x) dx + \int g(x) dx$  
 $\int k f(x) dx = k \int f(x) dx$  
 
-| $f(x)$ | $\int f(x) \cdot dx$ |
-| ------ | -------------------- |
-| $k$ (constant) | $kc + c$ |
-| $x^n (n \in J\\\{-1\})$ | ${1 \over {n+1}}x^{n+1} + c$ |
+| $f(x)$                          | $\int f(x) \cdot dx$         |
+| ------------------------------- | ---------------------------- |
+| $k$ (constant)                  | $kc + c$                     |
+| $x^n$         | ${1 \over {n+1}}x^{n+1} + c$ |
+| $1 \over x$ | $\log_e x + c$ |
+| $e^kx$ | ${1 \over k} e^{kx} + c$ |
+| $\sin kx$ | $-{1 \over k} \cos (kx) + c$ |
+| $\cos kx$ | ${1 \over k} \sin (kx) + c$ |
+| ${f^\prime (x)} \over {f(x)}$ | $\log_e f(x) + c$ |
+| $g^\prime(x)\cdot f^\prime(g(x)$ | $f(g(x))$ (chain rule)|
+| $f(x) \cdot g(x)$ | $\int [f^\prime(x) \cdot g(x)] dx + \int [g^\prime(x) f(x)] dx$ |
+